Lagrangian Point หรือ จุดลากรางจ์ บ้านของยานสำรวจอวกาศกว่าหลาย 10 ลำ หลายคนที่ติดตามข่าวของ Jame Webb Space Telescope หรือ JWST อาจจะพอเคยได้ยินคำว่า Lagrange มาบ้างว่า JWST จะถูกเอาไปโคจรอยู่ที่จุด L2 หรือ Lagrangian Point 2 แต่ว่าอาจจะยังไม่รู้ว่าทำไมถึงต้องเอาไปโคจรไว้ที่นั่นแล้วมันดีอย่างไร ในยทความนี้เราจะมพูดถึงคุณสมบัติของ Lagrangian Point และประโยชน์ต่าง ๆ ทางด้านดาราศาสตร์ของมัน
กลศาสตร์ท้องฟ้ากับลากรางจ์
การค้นพบจุดลากรางจ์เริ่มต้นมาจากปัญหาที่เรียกกันว่า Three-body problem ซึ่งเป็นการนำความเร็วและมวลของวัตถุสามวัตถุมาคำนวณหา Motion อ้างอิงตามกฏการเคลื่อนที่ของนิวตันและกฎความโน้มถ่วงสากลของนิวตันสิ่งที่ได้ก็คือ Chaotic Dynamical System หรือทฤษฎีเคออส ชื่อไทยก็ทฤษฎีความอลวน ทฤษฎีเคออสจะมีลักษณะที่ดูเหมือนว่าสุ่มมั่วหรือเละไปหมดแต่ความเป็นจริงแล้วมันไม่ได้สุ่มแต่เป็นระบบระเบียบแค่ดูเหมือนสุ่มเพียงเท่านั้น
Three-body problem เป็นหนึ่งใน Chaotic System ที่ดูเหมือนว่ามันไม่ได้มีระบบระเบียบอะไรเลย หากดูการจำลองข้างบนก็จะพบว่าวัตถุสามวัตถุเมื่อปล่อยให้เป็นไปตามกฎการเคลื่อนและกฎความโน้มถ่วงสากลของนิวตันแล้วจะพบว่าวัตถุทั้งสามมีวิธีโคจรที่ไม่แน่นอนและไม่มีความเป็นระบบ ระเบียบแม้แต่น้อย แต่ในความเป็นจริงแล้วการเคลื่อนที่ของวัตถุทั้งสามและวิถีโคจรมันเป็นระบบระเบียบ (Systematic) กล่าวคือในเมื่อมันอ้างอิงกฎการเคลื่อนที่วัตถุทั้งสามมันก็ต้องเคลื่อนที่ตามกฏแน่นอนแต่ปัญหาหลัก
คือเราไม่มีสูตรตายตัวที่จะนำมาคำนวณการเคลื่อนที่ของวัตถุที่มากกว่า 2 วัตถุขึ้นไป เรามีแค่สูตรที่ใช้คำนวณการเคลื่อนที่ของวัตถุสองวัตถุเท่านั้น เช่น F = G (m1m2/r^2)
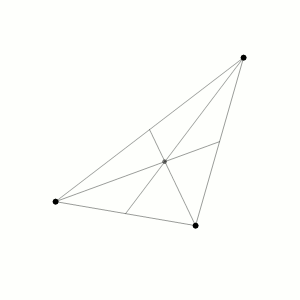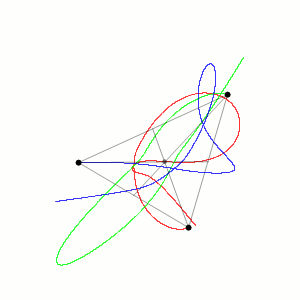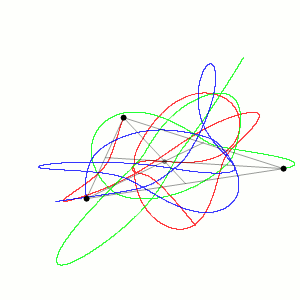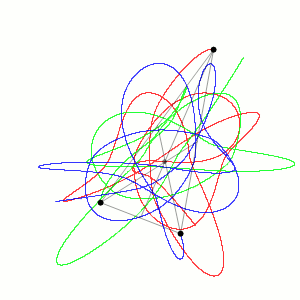
การไม่มีสูตรตายตัวในการคำนวณระบบที่มีมากกว่า 2 วัตถุขึ้นไปทำให้เราไม่ได้มีแค่ Three-body problem แต่เป็น n-body problem หมายความว่าเราจะมี Four-body problem, Five body problem ไปเรื่อย ๆ (เพราะฉะนั้นมันเลยไม่มีข้อสอบฟิสิกส์หรือโจทย์ฟิสิกส์แปลก ๆ ที่ให้คำนวณแรงดึงดูดหรืออะไรก็ตามของระบบวัตถุที่มีมากกว่า 2 วัตถุขึ้นไป)
ในปี 1772 นักคณิตศาสตร์ชื่อว่า Joseph-Louis Lagrange ได้พยายามคำนวณและหาวิธีแก้ Three-body problem ระหว่างการคำนวณเขากลับเจอจุดสมดุลใน Three-body problem แทนซึ่งเป็นจุดที่สามารถหาสูตรคำนวณได้อย่างตายตัวทำให้เกิดสิ่งที่เรียกว่า Restricted three-body problem โดยเป็นโมเดลที่อยู่ภายใต้ Configurations พิเศษ กล่าวคือเอาสูตรนี้ไปใช้กับสถานการณ์อื่นไม่ได้ Restricted three-body problem จะสมมุติให้มวลของวัตถุหนึ่งจาก 3 วัตถุมีสถานะเป็น “Negligible” กล่าวคือไม่สนและจะไม่เอามาคำนวณในสมการ เมื่อคำนวณ Restricted three-body problem ออกมาจะได้โมเดลที่มีจุด Equilibrium หรือจุดสมดุลทั้งหมด 5 จุด (จริง ๆ Leonhard Euler เจอก่อน 3 จุดคือ L1, L2 และ L3 แต่ Lagrange เจอเพิ่มเป็น L4 และ L5)
จุดสมดุลทั้ง 5 นี้เองมีชื่อเรียกว่า Lagrange Point 1,2,3,4 และ 5 สามารถย่อเป็น L1, L2, L3, L4, L5 ได้ จุดเหล่านี้เป็นจุดที่เมื่ออ้างอิงตามกฎความโน้มถ่วงสากลแล้วคือจุดที่วัตถุขนาดใหญ่ Exert แรงโน้มถ่วงต่อกันแล้วเกิดดุลยภาพขึ้น (Equilibrium) กับระบบ ดังนั้น Relative Position หรือตำแหน่งของจุด Lagrange จะอยู่ที่เดิมตลอดเวลาไม่ว่าทั้งระบบจะเคลื่อนที่แบบไหนก็ตาม จุด Lagrange ก็จะตามไปด้วย
แต่ 3 ใน 5 จุดนี้ คือ L1, L2 และ L3 เป็ดจุดที่ไม่เสถียร (Unstable) เพราะว่ามัน คือ “จุด” จริง ๆ มันเป็นแค่จุดที่มีขนาดเล็กมาก ให้นึกภาพว่ามัน คือ ยอดเขาแหลม ๆ L1, L2 และ L3 ก็คือจุดที่สูงที่สุดบนยอดเขาแหลม ๆ นั่นเอง ในขณะที่ L4 และ L5 ก็เป็นยอดเขาเหมือนกันแต่มันคือยอดเขาราบเรียบ (ฮา)
การค้นพับจุด Lagrange ในตอนนั้นก็ไม่ค่อยจะเป็นประโยชน์เท่าไรเพราะว่าในปี 1772 คนเขาก็ไม่รู้จะเอาการค้นพบนี้ไปทำอะไร แต่มันมีประโยชน์ในปัจจุบันเมื่อนักดาราศาสตร์นำทฤษฎี Lagrange มาใช้คำนวณหาจุด Lagrange ระหว่างโลกกับดวงอาทิตย์เราก็ได้จุด Lagrange ทั้ง 5 มาเช่นกันดังรูป
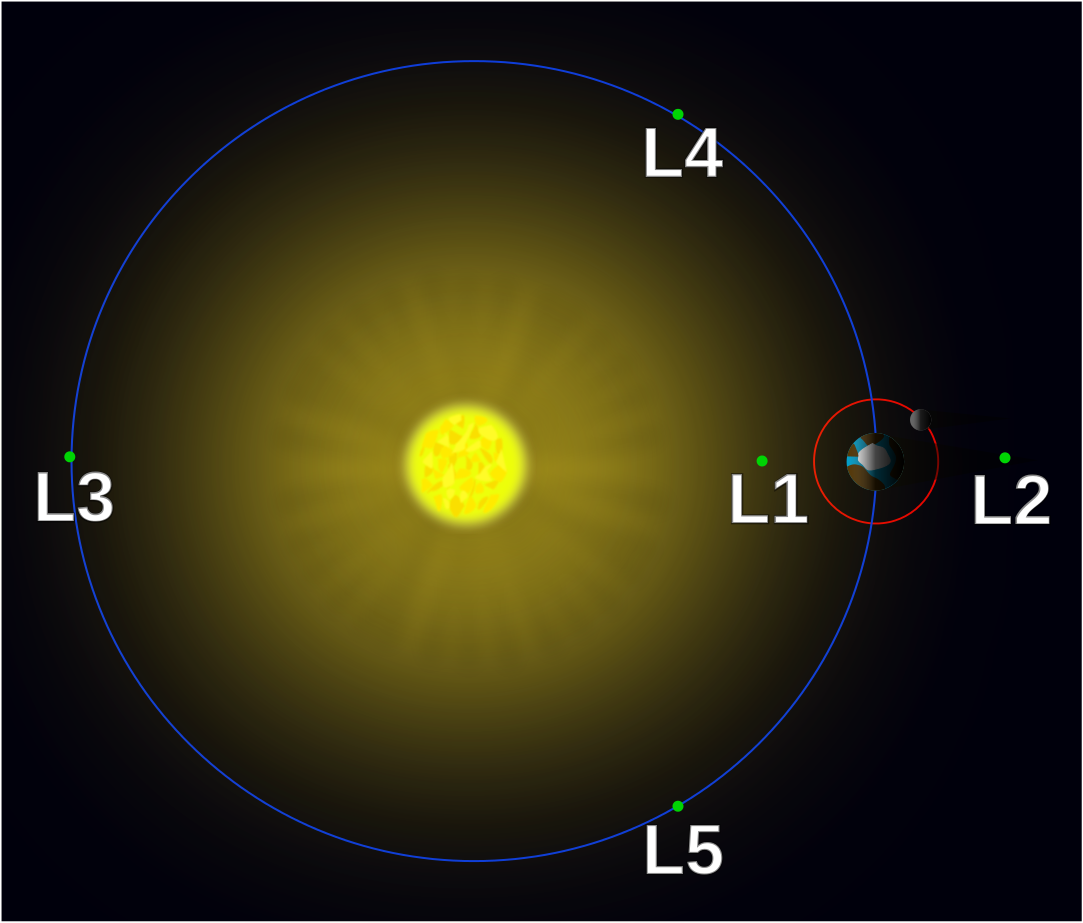
เมื่อนำ Lagrange มาประยุกต์กับฟิสิกส์วงโคจรเราก็จะได้จุดสมดุลที่เราสามารถนำดาวเทียมไป “จอด” ไว้ได้เพราะว่าจุด Lagrange จะเคลื่อนที่ไปตามระบบ Sun-Earth และดาวเทียมที่วางไว้ก็จะเคลื่อนที่ไปตามจุด Lagrange ตลอดเวลา ซึ่งเป็นประโยชน์ต่อการสำรวจเป็นอย่างมาก
จุด L1 เป็นจุดที่อยู่ข้างหน้าโลกตลอดเวลานั้นหมายความว่ามันจะเห็นดวงอาทิตย์ตลอดเวลาเช่นกันซึ่งเป็นประโยชน์ต่อการสำรวจดวงอาทิตย์ ปัจจุบันดาวเทียมที่โคจรอยู่ในตำแหน่ง L1 มีดังนี้
- Solar and Heliospheric Observatory (SOHO)
- Advanced Composition Explorer (ACE)
- WIND
- Deep Space Climate Observatory (DSCOVR)

จุด L2 เป็นจุดที่อยู่หลังโลกและหลังดวงจันทร์ เป็นบ้านของดาวเทียมและกล้องโทรทรรศ์อวกาศต่าง ๆ ที่ไม่ชอบแสงดวงอาทิตย์นั้นเองเพราะว่าจุด L2 จะมีโลกบังตลอดเวลาทำให้เกิดสุริยุปราคาตลอดเวลา (แต่ก็ยังมีแสงเข้าถึงนะ) ทำให้ยานที่อยู่ตรงนี้ถ้าอยากให้มืดขึ้นก็ต้องหาอะไรมาบังเพิ่มอย่าง JWST ก็จะมีแผ่นสะท้อนแสง (Sunshield) ขนาดใหญ่เพิ่มขึ้นมาเพื่อไม่ให้แสงอาทิตย์มารบกวนการถ่ายภาพวัตถุใน Deep Space เพราะว่าวัตถุ Deep Space นั้นค่อนข้างมองยากและมีความสว่างปรากฎต่ำ ถ้ามีแสงที่โคตรสว่างจากดวงอาทิตย์มาส่องก็ถ่ายไม่ได้เลยจำเป็นต้องเอา Shielding มากันเพิ่มเติมเพื่อให้มันมืดและเย็นขึ้น

คำถามเพิ่มเติมคือในเมื่อดาวเทียมหรือกล้องโทรทรรศน์อวกาศที่ว่านี่อยู่หลังโลกที่บังดวงอาทิตย์ตลอดเวลาทำให้เกิดสุริยุปราคาตลอดเวลาถึงจะไม่เต็มดวงแต่ก็ทำให้แสงจากดวงอาทิตย์ลดลงไปอย่างมาก แล้วแสงที่เหลือนี่พอสำหรับการแปลงไฟฟ้าด้วย Solar Panel หรือไม่ คำตอบคือโดยปกติวงโคจรของวัตถุใน Lagrange Point 2 จะไม่ได้อยู่หลังโลกตลอดเวลาแต่จะออกมารับแสงอาทิตย์เป็นระยะ ๆ อาศัยความไม่สมดุลในจุด L2 เพื่อออกไปรับแสงอาทิตย์ซึ่งจะอธิบายในส่วนต่อไป

ส่วนจุด L3 เป็นจุดที่อยู่ตรงข้ามกับโลกอยู่หลังดวงอาทิตย์ซึ่งจุดนี้ไม่มีใครบ้าเอาดาวเทียมหรืออะไรก็ตามไปวางไว้เพราะว่าเอาไปวางไว้ก็ไม่รู้จะใช้ทำอะไร ไกลก็ไกลแถมอยู่หลังดวงอาทิตย์ (ดูรูปประกอบระบบ Lagrange) สิ่งแรกที่ต้องถามเลยถ้ามีคนจะเอาดาวเทียมไปวางไว้ตรงนั้นจริง ๆ หนึ่งคือจะส่งไปยังไง? ทะลุดวงอาทิตย์ไปก็ไหม้เกรียมพอดี อ้อมไปก็เปลืองเชื้อเพลิง สองคือจะสื่อสารยังไง? ส่งสัญญาณทะลุดวงอาทิตย์ก็ไม่ได้เพราะดวงอาทิตย์บัง ต่อให้ส่งมาได้ก็ไม่รู้จะรับยังไงเพราะถ้าหันจานรับสัญญาณอย่างจานของ DSN ไปหาดวงอาทิตย์ก็ Sun Outage กันพอดี สัญญาณรบกวนมาเพียบ และสุดท้ายคือจะส่งไปทำอะไร เพราะถ้าส่งไปตรงนั้นสู่ส่งไป L4 หรือ L5 ไม่ดีกว่าหรอ ใกล้กว่าเสถียรกว่าแถมไม่ต้องมาลำบากเรื่องการสื่อสารด้วย

ส่วนจุด L4 และ L5 ปัจจุบันยังไม่มีดาวเทียมประจำอยู่ แต่เคยมีดาวเทียมไปบินผ่านมาแล้ว เช่น OSIRIS-REx ที่ผ่านแถบ L4 เพื่อไปสำรวจดาวเคราะห์น้อย หรืออย่าง Hayabusa 2 ที่ผ่านจุด L5 ในปี 2017 เพื่อไปหาสิ่งที่เรียกว่า Earth trojans หรือดาวเคราะห์น้อยที่โคจรในวงโคจรโลกนั้นเองซึ่งที่จุด L4 และ L5 คุณสมบัติของวงโคจรจะเป็นแบบเดียวกับวงโคจรของโลกกับดวงอาทิตย์นั้นเอง ทำให้วัตถุใดก็ตามที่อยู่ใน L4 และ L5 มีคาบโคจรเหมือนโลก ซึ่ง ณ ตอนนี้ ปี 2020 พบเพียงแค่วัตถุเดียวคือ 2010 TK7 ในจุด L4 เป็นดาวเคราะห์น้อยเส้นผ่านศูนย์กลางประมาณ 150 ถึง 500 เมตร ถูกพบโดย Wide-field Infrared Survey Explorer (WISE) ส่วน L5 ยังไม่พบไม่แต้ดวงเดียว
วงโคจรแปลก ๆ ใน Lagrange Point
หากใครเคยสังเกตวงโคจรของดาวเทียมในจุด Lagrange จะเห็นว่าวงโคจรมันจะแปลก ๆ คือวนไปวนมาอยู่บริเวณเดิมตลอดเวลาไป ๆ มา ๆ เป็นวงรีแถมมันโคจรรอบอะไรก็ไม่รู้ด้วยเพราะว่าตรงนั้นมันไม่มีวัตถุอะไรให้โคจรรอบ หากนึกภาพไม่ออกมันก็คือวงโคจรแบบนี้นั่นเอง และเหตุการณ์แบบนี้เกิดขึ้นกับทุกจุด Lagrange ทั้ง L1 และ L2
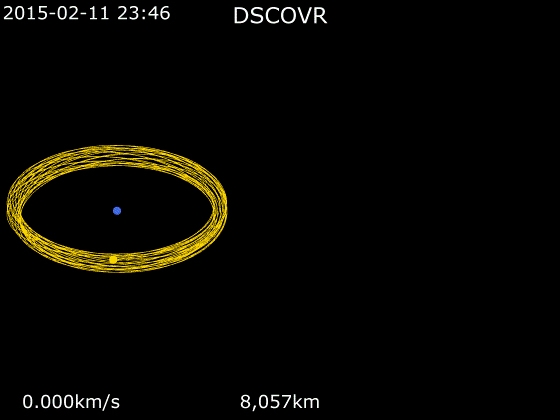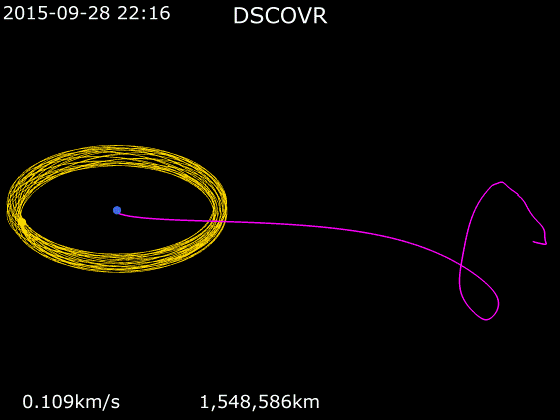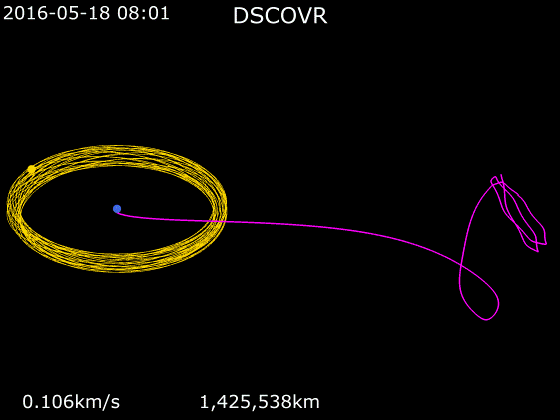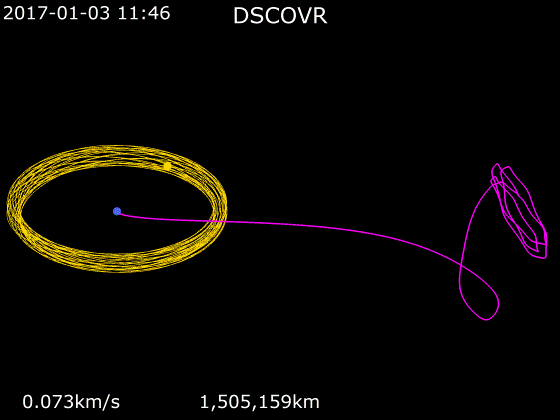

เหตุผลที่เป็นแบบนี้ก็เพราะว่าความไม่สมดุลของจุด Lagrange นั่นเอง จุด Lagrange ทั้ง 3 จุด คือ L1, L2 และ L3 คือจุด Lagrange ที่ไม่เสถียรอันเนื่องมาจากคุณสมบัติของตัวมันเองที่มีลักษณะเป็นเพียงแค่ “จุด” L1, L2 และ L3 มันคือจุดเล็ก ๆ เพียงจุดเดียวเท่านั้นที่สมดุล หากวางดาวเทียมคลาดเคลื่อนไปแม้แต่นิดเดียวมันก็จะไม่เสถียรทันทีและค่อย ๆ เสียสมดุล L1, L2 และ L3 เปรียบเสมือนจุดสมดุลบนลูกบอลแล้วเราพยายามเอาลูกแก้วไปวางบนลูกบอล มันจะไม่มีทางอยู่ในสภาวะที่เสถียร 100% ได้อย่างแน่นอนและเมื่อมันเริ่มไม่เสถียรมันก็จะเสียความเสถียรของตัวมันเองไปเรื่อย ๆ จนในที่สุดก็เสียสมดุลและค่อย ๆ กลิ้งตกจากลูกบอลช้า ๆ แล้วก็เร็วขึ้นเรื่อย ๆ นั้นเอง เหตุการณ์เดียวกันเกิดขึ้นกับจุด L1, L2 และ L3 เมื่อเราวางดาวเทียมไว้ยกตัวอย่างเช่นที่จุด L2 ดาวเทียมก็จะค่อย ๆ ขยับซ้ายหรือขวาไปทีละนิดเนื่องจากความไม่เสถียรแล้วพอมันขยับมันก็จะเสียสมดุลเพิ่มอีกไปเรื่อย ๆ จนในที่สุดมันก็จะหลุดจาก Lagrange Point ไป โดยปกติจุดเหล่านี้จะไม่เสถียรใน Time Scale ประมาณ 23 วัน เพราะฉะนั้นทุกประมาณ 23 วัน ดาวเทียมจำเป็นจะต้องจุดจรวดปรับทิศทางเพื่อดันตัวมันเองไปฝั่งตรงข้ามแล้วอีก 23 วันก็ดันกลับมาอีกวนเช่นนี้ไปเรื่อย ๆ จึงเป็นที่มาของวงโคจรแปลก ๆ รี ๆ วนไปวนมานั่นเอง ประโยชน์ของความไม่เสถียรนี่จริง ๆ ก็มีเหมือนกันคือสามารถใช้ความไม่สมดุลนี้เหวี่ยงดาวเทียมที่อยู่ใน L2 ออกไปให้แผงโซลาร์เซลล์รับแสงอาทิตย์เพื่อชาร์จแบตเตอรี่ได้เช่นกัน
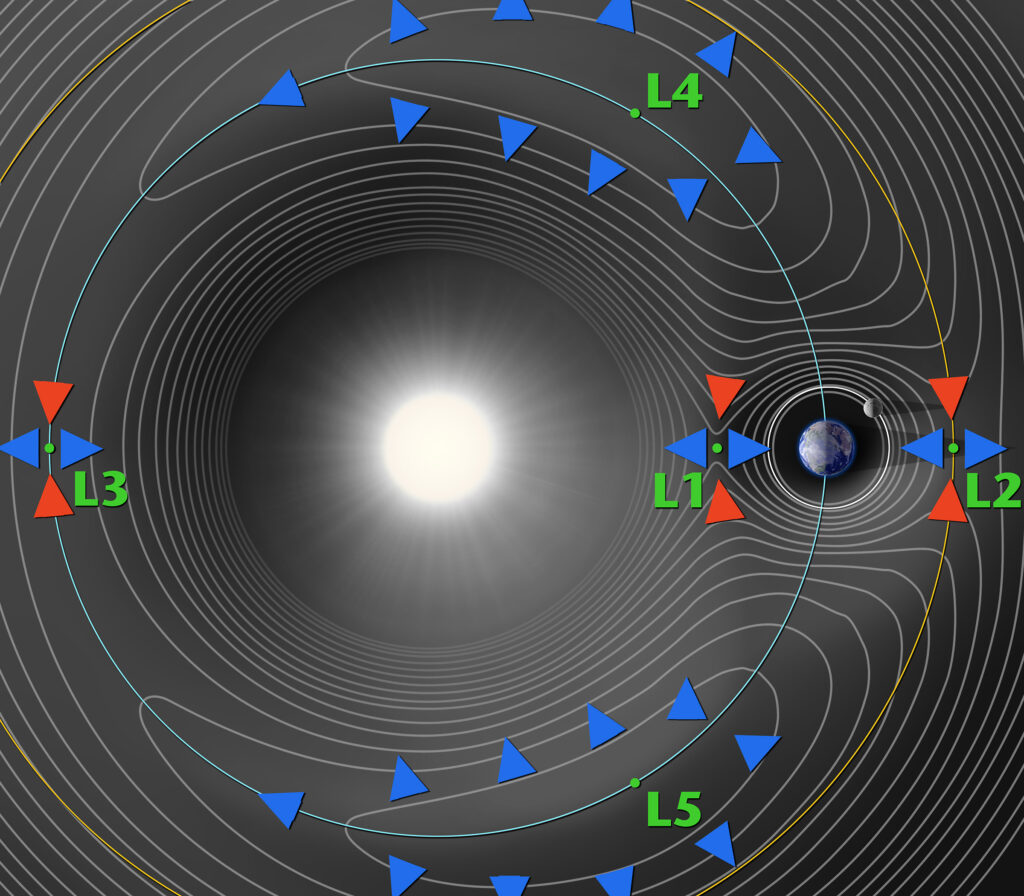
จริง ๆ L4 และ L5 ก็มีลักษณะคล้าย ๆ เนินเขาเช่นกันแต่เป็นเนินเขาที่ชันน้อยกว่า L1, L2 และ L3 ซึ่งแน่นอนว่าพอมันเป็นเนินเขาแสดงว่ามันก็ไ่ม่เสถียรคลาดเคลื่อนเมื่อไหร่มันก็จะค่อย ๆ เสียสมดุลจากช้า ๆ แล้วก็ค่อย ๆ เริ่มเร็วขึ้นเรื่อย ๆ เหมือนกัน แต่ที่ L4 และ L5 เสถียรอยู่เพราะว่ามันมีแรงพิเศษเรียกว่า Coriolis Force ที่ดันมันกลับที่เดิมไปสู่จุดสมดุล ยิ่งวัตถุเคลื่อนที่เร็วเท่าไหร่ Coriolis Force ที่เกิดจากการที่วัตถุจะพยายามที่จะไปตามทางที่มันเคยมา (ฮา) ผลก็คือวัตถุก็จะโดนดึงกลับไปที่จุดสมดุล
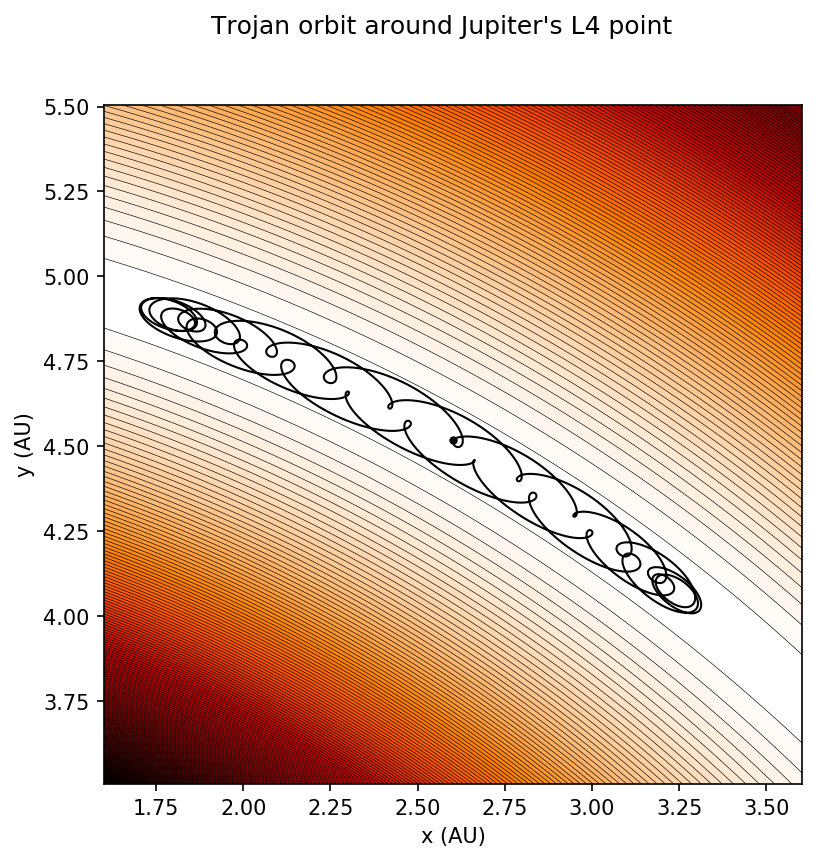
ผลก็คือวงโคจรจะถูกแรงที่จะเป็นเหมือน Barrier หรือกำแพงดันกลับไปสู่จุดสมดุลดันกันสลับไปสลับมาไปเรื่อย ๆ จึงทำให้วัตถุใน L4 และ L5 ไม่หลุดสมดุลนั่นเอง ปรากฏการณ์ Lagrange เกิดขึ้นกับทุก Two-body system กล่าวคือดวงจันทร์กับโลกก็มีจุด Lagrangian เช่นกัน คุณสมบัติเดียวกันทำให้ก็มีดาวเทียมที่อยู่ในจุด Lagrangian ในระบบ Earth-Moon เช่นกัน

หากใครยังนึกภาพของ Lagrangian Unstability หรือความไม่สมดุลของจุดลากรางจ์ไม่ออกให้ดูภาพนี้ อาจจะดูง่ายกว่า (แล้วทำไมไม่เอามาให้ดูตั้งแต่แรก ฮา) หากเปรียบเทียบพื้นที่ทั้งหมดบริเวณ L4 และ L5 ภายในลูกศรสีน้ำเงินคือเนินเขาที่ไม่ชันมาก ส่วน L1, L2 และ L3 เปรียบเสมือนลูกแก้วบนเส้นด้าย ที่ L1, L2 และ L3 เสียสมดุลได้ง่ายเป็นเพราะว่าจุดที่มันสมดุลจริง ๆ เป็นจุดที่เล็กมาก ๆ อารมณ์เหมือนพยายาม ๆ เอายางลบไปตั้งไว้บนดินสอแหลม ๆ นั้นแหละ ต่อให้ตั้งได้ลมพัดมานิดเดียวก็ร่วงแล้ว ซึ่งลมในที่นี่ก็สามารถเปรียบได้เป็นแรงภายนอกนั่นเอง ต่อให้เราสามารถเอาดาวเทียมไปวางไว้ที่จุดสมดุลของ Lagrange 1,2 หรือ 3 ได้สำเร็จ เมื่อไหร่ที่มีแรงภายนอกมากระทำมันก็จะหลุดสมดุลทันทีซึ่งแรงภายนอกในอวกาศก็มีมากมายนับไม่ถ้วนไม่จำกัดว่าต้องเป็นแรงโน้มถ่วงเพียงอย่างเดียวอาจจะลมสุริยะก็สามารถทำให้ดาวเทียมเสียสมดุลอันเล็กน้อยได้แล้ว ต่างกับ L4 และ L5 ที่ต่อให้หลุดสมดุลมันก็จะมีแรงเหมือนแม่เหล็กขั้วเดียวกันมาดันกลับให้ไปอยู่จุดสมดุลเหมือนเดิมทำให้มันไม่หลุดสมดุลนั่นเอง
เรียบเรียงโดย ทีมงาน SPACETH.CO
อ้างอิง
What is a Lagrange Point – NASA
Lagrange Points of the Sun-Earth system
Gravitational balance and stable configurations in rotating reference frames