Gravity หรือ ความโน้มถ่วงเอาจริงมนุษย์เราที่เดินดินบนโลกก็พอเข้าใจได้ว่าแรงโน้มถ่วงหรือความโน้มถ่วงโดยพื้นฐานคืออะไร มันคือแรงบางอย่างที่ดึงดูดทุกสิ่งทุกอย่างให้ตกลงสู่พื้นโลก เป็นแรงที่ทำให้ตัวติดพื้นโลก เป็นแรงที่ทำให้ดวงจันทร์โคจรรอบโลก เป็นแรงที่ทำให้โลกโคจรรอบดวงอาทิตย์ เป็นแรงที่เราเห็นและสัมผัสอยู่ทุกวันและเหมือนว่าเราจะเข้าใจมันดี แต่เรากลับแทบไม่เข้าใจอะไรเกี่ยวกับแรงนี้เท่าไหร่นัก
มนุษยชาติต้องใช้เวลายาวนานกว่า 20,000 ปีถึงจะเข้าถึงเศษเสี้ยวของความเข้าใจของสิ่งที่เราเรียกว่าความโน้มถ่วง และตอนนี้เรากำลังเข้าสู่จุดที่เรากำลังจะเข้าสู่ก้าวต่อไปในศาสตร์แห่งการศึกษาความโน้มถ่วง
แรงโน้มถ่วง หรือ ความโน้มถ่วง ?
เราควรเรียก Gravity ว่า “แรงโน้มถ่วง” หรือว่า “ความโน้มถ่วง” ? เอาจริงการเรียก Gravity ว่าแรงโน้มถ่วงหรือความโน้มถ่วงนั้นก็ไม่ได้แตกต่างกันเท่าไหร่นักหากคุณเดินออกไปคุยหน้าตลาดนัดกับเพื่อนของคุณหน้าร้านขายปลาดุก ถึงแม้ปลาดุกจะไม่เข้าใจถึงความแตกต่างระหว่างคำว่าแรงกับความ แต่สิ่งที่มันรับรู้ได้ขณะที่มันยังมีชีวิตอยู่และไหลไปตามน้ำก้นกะละมังคือความรู้สึกที่ตัวของมันถูกเร่งด้วยอะไรบางอย่าง เร่งมันให้สัมผัสกับพื้นกะละมังในอัตรา 9.8 m/s2 ตลอดเวลา ซึ่งมันอาจคิดว่ามีมือที่มองไม่เห็นดึงมันอยู่หรือโดนอะไรสักอย่างกดมันไว้ก็ไม่ผิด หรืออาจคิดว่าโดนแรงดึงเหนี่ยวรั้งเอาไว้ก็ไม่ได้ผิดอะไร ถึงแม้ว่ามันจะถูกหยิบออกมาจากพื้นกะละมังมาอยู่บนเขียงแล้วมันก็ยังสัมผัสได้ถึงแรงที่ดึง เร่ง และรั้งมันไว้เสมือนหนึ่งเป็นปกติ และถึงแม้มันจะพยายามหายใจบนเขียงต่อไปและสัมผัสได้ถึงแท่งไม้ที่มีความเร่งมากระทบหัวของมันอย่างเบา ๆ มันก็ยังคงถูกดึง เร่ง และรั้งด้วยแรงที่มันก็ไม่เข้าใจอยู่ดีอย่างเป็นปกติ

ทำไมเราต้องตกลงสู่พื้นดิน ไม่สามารถลอยได้อย่างอิสระ
การอธิบาย Gravity ในรูปแบบของแรง (Force) นั้นเป็นการอธิบายในกลศาสตร์คลาสสิค หรือรูปแบบที่เราพบเห็นได้ในชีวิตประจำวัน ซึ่งมันมิได้ผิดแผกไปจากความเป็นจริงเลย เราสามารถใช้กลศาสตร์คลาสสิคในการอธิบายสิ่งต่าง ๆ รอบตัวได้ดีมากทีเดียว ตั้งแต่การเดินเล่นในชีวิตประจำวันไปจนกระทั่งการส่งยานอวกาศไปยังดาวพฤหัสบดี ทั้งหมดสามารถอธิบายและคำนวนได้ด้วยกฎแรงโน้มถ่วงของนิวตันได้อย่างสบาย ๆ

ต่อมาเรามีทฤษฎีสมการสนามของไอสไตน์เข้ามาอธิบายเรื่องของความโน้มถ่วง มันสามารถที่จะอธิบายเรื่องราวของความโน้มถ่วงในสถานที่ที่มีความโน้มถ่วงสูงกว่าชีวิตประจำวันของเราได้ดีกว่ากฎของนิวตัน รวมถึงมันยังอธิบายปรากฏการณ์ที่เกี่ยวข้องกับเวลาและอวกาศต่าง ๆ ได้ ซึ่งกฎของนิวตันนั้นไม่สามารถอธิบายเหตุการณ์เหล่านี้ได้ แต่มิใช่ว่ากฎของนิวตันจะผิดหรือใช้งานไม่ได้แล้ว มันยังคงสามารถอธิบายในสถานที่ที่มีสภาพความโน้มถ่วงต่ำได้ดีเหมือนเดิมโดยที่เราไม่จำเป็นต้องนำทฤษฎีสนามของไอสไตน์มาคำนวนหรืออธิบายเลยด้วยซ้ำ
การเรียกความโน้มถ่วงว่าแรงโน้มถ่วงนั้นไม่ได้ผิดหรือทำให้คุณดูโง่กว่าเพื่อนของคุณที่เรียกว่าความโน้มถ่วงแต่อย่างไร เพราะในรูปแบบที่เราเจอในชีวิตประจำวันที่เราพบเจอเป็นลักษณะของ Weak Field ซึ่งไม่ได้เข้มข้นเหมือนอย่างพื้นที่โดยรอบข้างเคียงของหลุมดำหรือการอธิบายการเกิดความคาดเคลื่อนของเวลาเนื่องด้วยสภาพความโน้มถ่วงที่แตกต่าง ดังนั้นจึงไม่ผิดที่ในชีวิตประจำวันเราจะเรียกความโน้มถ่วงว่าแรงโน้มถ่วง แต่หากคุณกำลังอธิบายเรื่องราวของทฤษฎีสัมพัทธภาพแล้วก็ไม่ควรที่จะใช้คำว่า “แรงโน้มถ่วง” แทนคำว่า “ความโน้มถ่วง”
แรงโน้มถ่วงของนิวตัน
ความโน้มถ่วงในยุคของนิวตันนั้นเรายังนิยามความโน้มถ่วงในรูปแบบของแรง ๆ หนึ่งอยู่ ซึ่งนิวตันก็ยังอธิบายถึงหลักการทำงานของมันไม่ได้อย่างแน่ชัดว่าเพราะเหตุใดจึงเกิดแรงโน้มถ่วงในวัตถุที่มีมวลสาร แต่เขาอธิบายว่าแรงโน้มถ่วงนั้นทำงานอย่างไรในแนวคิดของแรงและพลังงานได้เป็นอย่างดีและดีมาก ๆ ซึ่งสมเหตุสมผลและพอใช้งานในชีวิตประจำวันได้เป็นอย่างดีจวบจนถึงการพานักบินอวกาศไปดวงจันทร์พร้อมกลับมา การใช้กฎแรงโน้มถ่วงของนิวตันในการอธิบายและคำนวนแรงในชีวิตประจำวันถึงเป็นเรื่องที่สมเหตุสมผล

ภาพวาดแสดงเส้นแรงโน้มถ่วงที่พุ่งเข้าสู่โลกตามกฎแรงโน้มถ่วงของนิวตัน
นิวตันอธิบายการทำงานของแรงโน้มถ่วงว่า เปรียบเสมือนแรงที่ปล่อยออกมาจากวัตถุที่มีมวลสารทุกวัตถุ โดยแรงนี้จะสามารถดึงดูดวัตถุที่มีมวลสารเหมือนกันได้และมันจะดึงดูดซึ่งกันและกันตามกฎการเคลื่อนที่ของนิวตันข้อที่ 3 ที่กล่าวว่า แรงกิริยา = แรงปฏิกิริยา ซึ่งสำหรับแรงกิริยาของแรงโน้มถ่วงของนิวตันนั้นคือแรงที่วัตถุ A ได้ออกแรงดึงดูดวัตถุ B และแรงปฏิกิริยาก็คือวัตถุ B ก็ออกแรงดึงดูดวัตถุ A เช่นกัน โดยแรงที่ทั้งสองต่างดึงดูดกันในลักษณะเส้นแรงที่ถูกแผ่ออกไปในทุกทิศทางในลักษณะของ 3 มิติ คือ บน ล่าง ซ้าย ขวา หน้า หลัง คล้ายสนาม โดยอธิบายให้เข้าใจง่าย ๆ คือสมมุติว่าวัตถุก้อนหนึ่งแผ่เส้นแรงออกไป 24 เส้นรอบทิศทางในรูปแบบ 2 มิติ หากคุณวัดปริมาณเส้นแรงต่อพื้นที่ a ในระยะห่าง h เราอาจจะวัดเส้นแรงที่แผ่ออกมาจากวัตถุนั้นได้ 3 เส้น แต่ถ้าเราเลื่อนตัวออกมาเป็นระยะ 2h และใช้พื้นที่ในการวัดเท่าเดิม เราจะได้เส้นแรงน้อยลงอาจจะเหลือ 2 เส้นแรง หรือ 1 เส้นแรงก็ได้ ซึ่งหากต้องการให้ปริมาณเส้นแรงเท่าเดิมในระยะ 2h เราต้องเพิ่มพื้นที่ a เป็น a2 เพื่อให้ปริมาณเส้นแรงที่เราวัดได้เท่าเดิม ตาม Inverse-square law
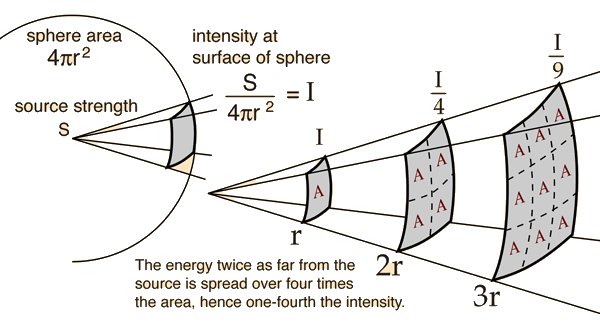
Inverse Square Laws ที่ถูกนำไปใช้กับทั้งแรงโน้มถ่วง แรงไฟฟ้า และแสง
ดังนั้นกฎความโน้มถ่วงสากลของนิวตันจึงได้เขียนสมการอธิบายว่า ขนาดสัดส่วนโมเมนตัมของแรงโน้มถ่วงนั้นเกิดจากผลคูณของมวลวัตถุสองก้อนผกผันกับระยะห่างของวัตถุทั้งสองก้อนเป็นค่ากำลังสอง
สัมพัทธภาพบนความปกติ
ทฤษฎีสัมพัทธภาพของไอสไตน์นั้นอย่างที่เราพอจะรู้กันว่าเราแบ่งทฤษฎีออกเป็นสองบทด้วยกัน คือ ทฤษฎีสัมพัทธภาพพิเศษ และ ทฤษฎีสัทพัทธภาพทั่วไป ถามว่าสองทฤษฎีบทนี้แตกต่างกันอย่างไร
ซึ่งตัวทฤษฎีนั้นสอดคล้องกันอย่างสวยงาม ซึ่งความแตกต่างของสองบทนี้คือ ความโน้มถ่วง
หากเป็นทฤษฎีสัมพัทธภาพพิเศษนั้นจะอธิบายปรากฏการณ์ของผู้สังเกตการณ์ในสภาวะปกติที่ปราศจากการรบกวนของความโน้มถ่วงและ/หรือความเร่งที่ทำให้ผู้สังเกตการณ์สังเกตอย่างผิดเพี้ยนไปจากกฎของฟิสิกส์ ส่วนทฤษฎีสัมพัทธภาพทั่วไปนั้นจะอธิบายถึงผู้สังเกตการณ์ที่ตรวจวัดนั้นอยู่ในพื้นที่และบริเวณที่ไม่เป็นปกติอันเป็นผลเนื่องจากการได้รับความโน้มถ่วงและ/หรือความเร่งบางประการทำให้ผู้สังเกตการณ์สังเกตเห็นรูปแบบของเหตุการณ์ผิดเพี้ยนไปจากกฎของฟิสิกส์ ดังนั้นหากต้องการที่จะอธิบายเรื่องราวของความเร่งและความโน้มถ่วงแล้ว (ซึ่งจริง ๆ แล้วเป็นสภาวะที่ปกติในโลกความเป็นจริงแต่ไม่ปกติในโลกของฟิสิกส์) เราจะใช้ทฤษฎีสัมพัทธภาพทั่วไปในการอธิบายถึงเหตุการณ์เหล่านั้น
ความโค้ง = ความโน้มถ่วง
นิยามในเชิงของความโน้มถ่วงโดยไอสไตน์นั้นได้อธิบายว่า ความโน้มถ่วงนั้นเกิดจากการที่อวกาศเกิดการโค้งงอขึ้นจากพลังงานและมวลสาร ดังนั้นหากอวกาศไม่โค้งก็เท่ากับสภาพแวดล้อมบริเวณนั้นไม่มีความโน้มถ่วง แต่หากสภาพแวดล้อมบริเวณนั้นอัดแน่นไปด้วยพลังงานอันมหาศาลและมวลสารที่หนาแน่นสูงละก็ อวกาศบริเวณนั้นก็จะถูกบิดเบือนโค้งไปตามพลังงานและมวลสารนั้น ตามสมการสนามของไอสไตน์

การทดลองสมมุติการเกิดความโน้มถ่วงโดยใช้ลูกบอลเหล็กหนักมาวางบนผืนผ้าใบที่ถูกขึงให้ตึง
หากเราเปรียบอวกาศเป็นเหมือนผืนผ้าแทมโพลีนที่ยืดหยุ่นและถูกขึงตรึงไว้กับขอบแล้ว เมื่อเราหย่อนมวลลงไปยังผืนผ้าแทมโพลีนมันย่อมจะยืดออกตามน้ำหนักของมวลก้อนที่เราหย่อนลงไปและมวลนั้นถูกต้านด้วยแรงตึงของเส้นใยของผืนผ้า ลักษณะของผืนผ้าใบที่โค้งจนเป็นหลุมนี้คืออวกาศที่โค้งเพราะมวล เราจึงสามารถเปรียบได้ว่ามันคือความโน้มถ่วง

กาลอวกาศที่ถูกบิดโค้ง ที่มา – The Museum of Nature & Science
สภาพความเร่งกับความโน้มถ่วง
เราอยู่บนโลกที่มีความโน้มถ่วงเร่งเราให้ตกถึงพื้นที่ความเร่ง 9.8 m/s2 ซึ่งเป็นปกติอยู่แล้ว แต่หากคุณเข้าไปอยู่ในห้องที่ปิดสนิททึบไม่สามารถมองเห็นภายนอกได้แล้วผมจุดจรวดใต้ห้องนั้นให้เคลื่อนที่ภายในอวกาศด้วยความเร่งเท่ากับความโน้มถ่วงของโลก ผมสามารถพูดได้เลยว่าคุณไม่สามารถแยกออกได้ว่าคุณกำลังยืนอยู่บนโลกนิ่ง ๆ หรือเคลื่อนที่ไปพร้อมกับจรวดที่มีความเร่งที่เท่ากับความโน้มถ่วงของโลกอยู่ นี่คือสภาพของความโน้มถ่วงจากความเร่ง

ภาพแสดงให้เห็นว่าเมื่อเราอยู่ในกล่องที่ปิดทึบไม่สามารถมองเห็นภายนอกได้ ไม่ว่าจะอยู่บนโลกหรือบนจรวดที่เคลื่อนที่ด้วยความเร่งคงที่ก็จะรับรู้ได้ถึงความเร่งอย่างที่ไม่แตกต่างกันแม้แต่น้อย
เช่นกัน หากคุณเคยตกจากที่สูงแบบ free fall เช่นการกระโดดจากตึกหรือการกระโดดดิ่งพสุธาเล่นนั้น คุณจะมีความเร่งในการตกเท่ากับ 9.8 m/s2 และในช่วงเวลาที่คุณกำลังถูกเร่งให้ตกอยู่นั้นคุณจะไม่สามารถรับรู้ได้ถึงน้ำหนักของตัวเองหรือแม้แต่ความโน้มถ่วงได้เลย ดังนั้นในสภาวะตอนนั้นสามารถเรียกได้ว่าอยู่ในสภาวะไร้ความโน้มถ่วงได้ เช่นเดียวกับห้องปิดตายจุดจรวด หากเราให้คุณเข้าไปในห้องแล้วเตะห้องนั้นลงจากจรวดให้ตกลงไปยังโลก ระหว่างที่กล่องลอยอยู่กลางอากาศ สภาพภายในกล่องนั้นสามารถเรียกว่าสภาพไร้ความโน้มถ่วงสมบูรณ์เช่นเดียวกับการที่คุณลอยอยู่กลางอวกาศไกลที่ปราศจากความโน้มถ่วง คุณไม่สามารถแยกออกได้ว่าตอนนี้คุณอยู่ที่ไหนได้อย่างสมบูรณ์
ซึ่งต่อให้คุณพยายามหาทางพิจารณาอย่างไรเพื่อให้สามารถอธิบายเหตุการณ์ภายนอกด้วยการทดลองภายในห้อง ข้อมูลที่คุณได้ย่อมไม่สามารถบอกได้ว่าแท้จริงแล้วสภาพตอนนี้ภายนอกนั้นเป็นอย่างไรนอกจากจะยื่นหัวออกไปจากห้องแล้วสังเกตว่าเกิดอะไรขึ้น
เวลาและอวกาศนั้นสัมพันธ์กัน
มนุษย์พยายามที่จะหาคำตอบของมิติที่สูงขึ้นไปจากมิติที่ตนเองอาศัยอยู่เพื่ออธิบายบางเหตุการณ์ตามธรรมชาติหรือทางฟิสิกส์ทฤษฎี กาลอวกาศเป็นทฤษฎีที่ดีที่สุดที่มนุษย์พยายามหาสิ่งที่เป็นไปได้มาอธิบายเรื่องราวของมิติที่สูงกว่าตนเองคือเรื่องราวของ Minkowski space
Minkowski space เป็นทฤษฎีฟิสิกส์ปริภูมิเวลาของ Hermann Minkowski นักฟิสิกส์ทฤษฎีชาวเยอรมณี ซึ่งเขาได้ใช้แนวคิดของทฤษฎีสัมพัทธภาพมาช่วยในการอธิบายเรื่องของอวกาศแบบยูคลิตสามมิติมาผนวกกับเวลาตามแนวคิดของไอสไตน์
เมื่อเขาผสานเรื่องของปริภูมิสามมิติของยูคลิตเข้ากับปริภูมิเวลาเข้าด้วยกัน จึงเกิดเป็นมิติที่เกี่ยวเชื่อมโยงกันอย่างแน่นแฟ้นไม่สามารถที่จะแยกออกจากกันได้ จึงเกิดเป็นสิ่งที่เรียกว่า Spacetime
Spacetime หรือกาลอวกาศนั้นเป็นความเกี่ยวเนื่องกันของอวกาศพื้นหลังกับเวลานั้นเกิดและเคลื่อนไหวไปพร้อม ๆ กัน หากอวกาศพื้นหลังเกิดการเคลื่อนไหวหรือบิดเบี้ยว เวลาในบริเวณที่ได้รับผลกระทบย่อมบิดเบือนไปพร้อมกับอวกาศด้วย ดังนั้นเมื่อมวลสารและพลังงานสร้างความโค้งที่อวกาศ เวลาจึงบิดเบือนไปตามอวกาศที่โค้ง ยิ่งอวกาศมีความโค้งมากยิ่งยวดเท่าใด เวลาย่อมมีความเปลี่ยนแปลงมากตามอวกาศเท่านั้น
ความโน้มถ่วง + กลศาสตร์ควอนตัม ในเปลือกนัท
ศาสตร์ของสัมพัทธภาพนั้นเป็นศาสตร์หนึ่งที่เปลี่ยนแปลงความเข้าใจที่มนุษยชาติมีต่อมุมมองของเอกภพนี้ไปอย่างยวดยิ่ง แต่ตัวทฤษฎีสัมพัทธภาพนั้นก็ยังไม่สามารถอธิบายเรื่องราวความเป็นไปของเอกภพทั้งหมดได้อย่างสมบูรณ์และสวยงาม

ทฤษฎีสัมพัทธภาพนั้นอธิบายเรื่องราวของสสารที่มีขนาดใหญ่ได้ดีอย่างมหัศจรรย์ ไม่ว่าจะเป็น หลุมดำ ดาวนิวตรอน หรือ ดวงอาทิตย์ แต่มันกลับไม่สามารถอธิบายเรื่องราวที่มีขนาดเล็กได้ดีนักอย่าง อะตอม อนุภาคมูลฐาน หรือ พฤติกรรมของควาร์กได้เลย ผิดกับกลศาสตร์ควอนตัมที่อธิบายเรื่องราวของสิ่งเล็ก ๆ ได้อย่างสวยงามแต่ก็ไม่สามารถอธิบายเรื่องราวของสิ่งใหญ่ ๆ อย่างสัมพัทธภาพได้เลย
เหมือนจะเป็นจุดที่เกิดปัญหาเพราะเมื่อเอกภพเป็นอย่างที่มันเป็นไปแต่มนุษย์ไม่สามารถอธิบายเรื่องราวต่าง ๆ ได้อย่างที่ควรจะเป็นเพียงเพราะทฤษฎีที่จะอธิบายเรื่องราวทั้งสองไม่สามารถผสานรวมกันได้ จึงต้องใช้ศาสตร์ทางคณิตศาสตร์มาช่วยในการทำให้ทั้งสองทฤษฎีพอที่จะรวมกันและอธิบายได้อย่างสมเหตุสมผล
หากไม่เข้าใจเราอาจจะลองยกตัวอย่างเหตุการณ์ที่ต้องใช้ถึงสองกลศาสตร์ในการอธิบายอย่างหลุมดำ หลุมดำเป็นสถานที่สุดวิเศษในเอกภพ เพราะมันเป็นสถานที่สุดมหัศจรรย์ที่เราต้องใช้ถึงสองทฤษฎีในการอธิบายมัน

หลุมดำเป็นพื้นที่วิเศษที่อวกาศบริเวณนั้นเกิดการโค้งอย่างรุนแรงจนค่าความโค้งเป็นอนันต์หรือที่เรียกกันว่า Gravitational-Singularity หรือภาวะเอกฐานเชิงความโน้มถ่วง ซึ่งบริเวณนั้นกาลอวกาศไม่สามารถที่จะดำเนินต่อไปได้ และเมื่อความโน้มถ่วงที่มหาศาลขนาดนั้นย่อมสามารถที่จะเหนี่ยวรั้งทุกสิ่งทุกอย่างแม้แต่แสงไม่ให้สามารถหลุดออกไปได้ บริเวณนั้นจึงมืดมิดที่สุดอย่างหาเปรียบมิได้ แต่ถึงเช่นนั้นหลุมดำกลับไม่สามารถดูดอะไรเข้าไปภายใน Singularity ได้เลยเพราะว่าเมื่อสสารหรือพลังงานเข้าไปถึงขอบฟ้าเหตุการณ์แล้วพื้นหลังจากขอบฟ้าเหตุการณ์นั้นไม่มีแม้กระทั่งเวลา ดังนั้นเมื่อสสารลอยเข้ามาถึงขอบฟ้าเหตุการณ์มันจะติดอยู่แค่บริเวณนั้นไม่สามารถไปต่อได้ เหมือนท่อระบายน้ำที่ฝาท่อเปิดอยู่แต่น้ำกลับไม่ลงไปตามท่ออย่างไรอย่างนั้น ซึ่งหากเป็นเช่นนั้นแสดงว่าไม่เคยมีอะไรเข้าไปในหลุมดำแม้แต่เศษเสี้ยวของอนุภาคเดียว ซึ่งสิ่งนั้นเป็นไปไม่ได้ตามหลักความเป็นจริง

ดังนั้นเราจึงต้องใช้กลศาสตร์ควอนตัมในการอธิบายหลุมดำที่ไม่ใช่เชิงความโน้มถ่วงแต่เป็นเชิงจุดแทน เพราะ Singularity นั้นอยู่ในสภาพที่เป็นจุดดังนั้นมันจึงไม่สามารถอธิบายในส่วนของสัมพัทธภาพได้อย่างสมบูรณ์ กลศาสตร์ควอนตัมเข้ามาอธิบายเหตุการณ์ที่สสารและพลังงานหลุดเข้าไปในขอบฟ้าเหตุการณ์แล้ว ซึ่งแสดงว่าสสารและพลังงานนั้นสามารถที่จะหลุดเข้าไปในภายใน Singularity ได้ซึ่งทำให้ภาพของหลุมดำนั้นสมบูรณ์แบบมากยิ่งขึ้น แต่ถึงกระนั้นเรื่องราวของหลุมดำก็ยังคงมีปัญหาอยู่คือ สสารและพลังงานไม่เคยสูญสลายไปจากเอกภพนี้นอกจากมันจะเปลี่ยนรูปเท่านั้น ดังนั้นสสารและพลังงานที่ตกลงไปภายในนั้นถือว่าหายไปอยางสมบูรณ์หรือไม่ ข้อถกเถียงภายในปัจจุบันของนักฟิสิกส์ทฤษฎีหลุมดำคือเราจะอธิบายถึงสสารที่หายไปภายในหลุมดำอย่างไรจึงจะสมเหตุสมผลตามเทอร์โมไดนามิก
ซึ่งอย่างที่เราเห็นกันว่าทฤษฎีสัมพัทธภาพและกลศาสตร์ควอนตัมนั้นเกี่ยวเนื่องและมีความเชื่อมโยงกันอย่างแน่นแฟ้นและแยกจากกันมิได้ แต่ในทางคณิตศาสตร์เมื่อเราพยายามที่จะหาทางให้สองทฤษฎีบทนี้มาผสานรวมกันกลับเป็นเรื่องที่เป็นไปไม่ได้เลย เรามักพบความยุ่งเหยิงและค่าที่เป็นอนันต์เสมอที่คำนวน นักฟิสิกส์จึงพยายามที่จะหาทางที่จะสร้างกฎหรือทฤษฎีใหม่ที่สามารถรวมทั้งสองทฤษฎีหรืออธิบายอย่างทั้งสองทฤษฎีให้ในทฤษฎีหรือสมการเพียงสมการเดียวให้จงได้ จึงเกิดเป็นทฤษฎีที่หลากหลายอย่างที่จะยกตัวอย่างต่อไปนี้สิ่งแต่ละทฤษฎีเป็นเสมือนเส้นทางที่แตกต่างกันโดยที่เราไม่รู้ว่าเส้นทางไหนจะนำพาเราไปสู่ความจริงของเอกภพ
มหากาพย์ทฤษฎีที่เป็นไปได้
นักฟิสิกส์ทฤษฎีพยายามอย่างหนักที่จะหาทฤษฎีที่อธิบายเรื่องราวต่าง ๆ ในมุมมองของสัมพัทธภาพและกลศาสตร์ควอนตัม จึงเกิดเป็นทฤษฎีใหม่ ๆ มากมาย ซึ่งหากกล่าวภายในบทความนี้คงสามารถที่จะตีพิมพ์หนังสือได้จบเล่มหนึ่งเป็นแน่ (เพราะแค่ตอนนี้ก็โคตรจะเยอะแล้ว) จึงหยิบยกทฤษฎีที่น่าสนใจมาอธิบายอย่างคร่าว ๆ
ทฤษฎีควอนตัมโฟม เป็นทฤษฎีแรก ๆ ที่พยายามนำทฤษฎีสัมพันธภาพมาผสานกับกลศาสตร์ควอนตัมจากพฤติกรรมบางประการของอวกาศ โดยทฤษฎีกล่าวว่าแท้จริงแล้ว Spacetime ที่ราบเรียบนั้นแท้จริงแล้วความราบเรียบนั้นไม่ได้ราบเรียบอย่างแท้จริงเมื่อเรามองลงไปให้เล็กอย่างเพียงพอระดับควอนตัมแล้วเราจะพบว่ากาลอวกาศนั้นไม่ได้ราบเรียบอย่างแท้จริงแต่เต็มไปด้วยคลื่นและฟองของควอนตัมที่มีลักษณะคล้ายมหาสมุทรของโลก หากเรามองจากอวกาศแล้วมหาสมุทรของโลกนั้นแทบราบเรียบเป็นผืนเดียวกัน แต่หากเราอยู่กลางมหาสมุทรเราจะพบว่ามหาสมุทรนั้นไม่เคยนิ่งเลย แต่เต็มไปด้วยคลื่นที่เคลื่อนไหวตลอดเวลา และมีฟองลอยออกมาคล้ายน้ำอัดลมที่ฟองอากาศลอยอยู่เหนือผิวน้ำและค่อย ๆ แตกฟองก่อนจะมีฟองใหม่มาอย่างสม่ำเสมอ ซึ่งความเล็กของควอนตัมโฟมที่อธิบายมานี้นักฟิสิกส์คาดว่าน่าจะมีขนาดที่เล็กกว่าขนาดของอะตอมถึง หนึ่งล้านล้านเท่า ซึ่งขนาดที่เล็กระดับนี้ย่อมยากที่จะตรวจจับได้ด้วยเครื่องตรวจจับอนุภาคในปัจจุบัน

ภาพจำลองจินตนาการของ ควอนตัมโฟม ที่ต่อให้ความเป็นจริงมันก็ไม่มีทางเป็นเช่นนี้และอยู่นอกเหนือสามัญสำนึกของเรา ที่มา – NASA/JPL
ทฤษฎี Entropic-gravity เป็นอีกหนึ่งทฤษฎีโดย Erik Verlinde โดยเขาได้เสนอทฤษฎีนี้ในปี 2009 โดยเขาได้เสนอทฤษฎีว่า ความโน้มถ่วงหรือความโค้งของกาลอวาศนั้นเกิดจากการเปลี่ยนแปลงของเอนโทรปีของระบบ โดยตามกฎของเทอร์โมไดนามิกนั้นเอนโทรปีภายในระบบนั้นจะเพิ่มขึ้นอย่างเป็นปกติ และปกติของมันนั้นปกติอย่างสมเหตุสมผล
ทฤษฎีสตริง กล่าวว่าเอกภพนั้นประกอบไปด้วยสิ่งที่เรียกว่าเส้น โดยเส้นเหล่านั้นมีขนาดเล็กระดับควอนตัมที่จะคอยสั่นตามความถี่ โดยแต่ละเส้นที่มีความถี่ที่แตกต่างกันนั้นสร้างเป็นข้อมูลทำให้เกิดเป็นภาพของอนุภาคมูลฐาน อิเล็กตรอน เกิดเป็นอะตอม เกิดเป็นกาลอวกาศ เกิดเป็นมนุษย์ เกิดเป็นโลก เกิดเป็นเอกภพ เป็นหนึ่งในทฤษฎีที่ยิ่งใหญ่มากทฤษฎีหนึ่งที่พยายามที่จะเป็นทฤษฎีสรรพสิ่งที่จะอธิบายทุกสิ่งทุกอย่างในเอกภพด้วยทฤษฎีเดียว
สรุป ความแตกต่างของแรงโน้มถ่วงของนิวตันและความโน้มถ่วงของไอสไตน์
เราอาจเปรียบเทียบความแตกต่างของแรงโน้มถ่วงของนิวตันกับความโน้มถ่วงของไอสไตน์ได้ เราอาจจะเปรียบเทียบความแตกต่างมันกับการแสดงละครภายในโรงละคร
กฎแรงโน้มถ่วงของนิวตันนั้นเปรียบเสมือนวัตถุที่มีมวลเป็นนักแสดงที่เคลื่อนที่ไปตามอวกาศที่เราเปรียบคือพื้นเวทีภายในโรงละคร นักแสดงบนเวทีย่อมมีความสัมพันธ์กันอย่างเป็นปกติ ส่วนทฤษฎีสัมพัทธภาพของไอสไตน์นั้นเปรียบเสมือนวัตถุที่เป็นนักแสดงที่เคลื่อนที่ไปบนเวทีของโรงละครที่เราเปรียบเสมือนกาลอวกาศ โดยสัมพัทธภาพจะอธิบายว่าตัวนักแสดงนั้นจะสัมพันธ์กับพื้นเวทีอย่างแยกจากกันไม่ได้ พื้นเวทีทำให้นักแสดงเคลื่อนที่และนักแสดงเคลื่อนที่ทำให้พื้นเวทีเกิดความเปลี่ยนแปลง อีกทั้งนักแสดงทุกคนบนเวทียังส่งผลกระทบให้กับเวทีและนักแสดงที่แสดงร่วมกันอย่างแบ่งแยกไม่ได้
อ้างอิง
หนังสือ How come to Know the Cosmos – Dr Helen Klus













